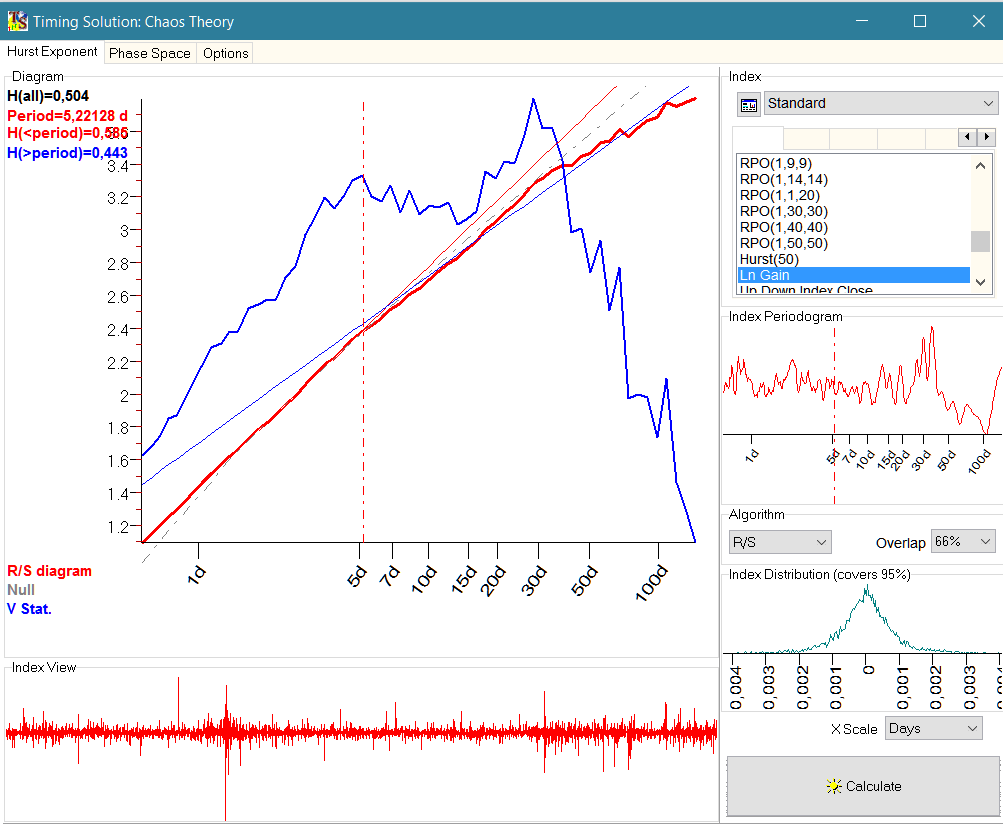
Модуль Chaos Teory

Идея модуля

Теория Хаоса – достаточно молодая математическая область, создание которой приравнивают по значимости открытий ХХ века к созданию квантовой механики. Почему разработки Херста (а именно они лежат в основе этого модуля) относятся к Теории Хаоса? И откуда такое название? Дело в том, что в этой теории берутся некие временные ряды (например, котировки), а потом мы пытаемся понять, в какой их части анализируемые данные имеют хаотичный характер, а в какой нет. Иначе говоря, мы выясняем, где во временных данных царит хаос, а где проглядывается некий относительный порядок (с математической точки зрения, хаос и порядок – понятия не взаимоисключающие). Почему нам так важно это понять? Потому что “хаотичные” периоды в котировках плохо прогнозируемы; а вот в “упорядоченных” периодах вполне можно выявить некую структуру (циклы), которую затем можно продлить или спроецировать в будущее. Тем самым мы пытаемся спрогнозировать поведение наших временных рядов, выявляем паттерны, работающие и за временной границей.

В модуле Chaos Teory нашли отображение идеи изложенных в книгах Эдгара Петерса (Edgar E. Peters): “Хаос и порядок на рынках капитала" (Chaos and order in the capital market) и “Фрактальный анализ финансовых рынков” (Fractal market analysis). Он считал, что рынки имеют фрактальную структуру, и в первую очередь - рынки Форекс. Валюта, по его мнению, имеет статистические и фундаментальные характеристики, которые отличают ее от других процессов. По существу, валюта не является ценной бумагой, хотя в отношении нее осуществляется активная торговля. Крупнейшие участники, центральные банки не представляют собой максимизаторов доходности; их цели не обязательно соответствуют целям рациональных инвесторов. В то же время на рынках валюты мало признаков стабильных циклов, хотя они действительно имеют сильные тренды.

На основании этих характеристик, взятых вместе, Петерс делал вывод, что валюта – истинный процесс Херста. То есть она характеризуется процессами бесконечной памяти. Долгосрочные инвесторы должны опасаться относиться к валюте так, как они относятся к другим активам. В частности, они не должны предполагать, что стратегия с покупкой и длительным владением будет выгодна в долгосрочной перспективе. Риск увеличивается во времени и не уменьшается со временем. Долгосрочному инвестору, который должен иметь валютный риск, следует рассмотреть активную торговлю такими активами. Они не предлагают никакого преимущества в долгосрочной перспективе.

Для торговли такими активами особенно важно иметь представление о персистентности, или долговременной памяти рынка, в торгуемых котировках; кроме того важно иметь непредвзятую экспертизу, которая может помочь оценить длину периодических или непериодических циклов (иначе говоря, выявить так называемый стохастический цикл).

Модуль Chaos Teory как раз и предоставляет такую возможность, прежде всего, через такой ключевой элемент теории Хаоса, как R/S-анализ. Устойчивый относительно шумов, R/S-анализ особенно привлекателен для изучения естественных временных рядов и, в частности, рыночных данных.

Вкладка Hurst Exponent

На данной вкладке мы ведем работу с главный аспектом теории хаоса — экспонентой Херста.

Поле Diagram

Перед нами графический результат «анализа масштабируемого диапазона» (Rescaled Range Analysis). Данная техника была разработана английским инженером-гидрологом, участвовавшем в строительстве Асуанской плотины в Египте, Харольдом Хёрстом (Harold Edwin Hurst) в 1965 году и представляет собой статистический метод анализа больших временных рядов, прилагаемый к так называемой экспоненте Хёрста (H), которая, в свою очередь, измеряет силу тренда в фрактальном броуновском движении.

Из левого нижнего угла исходят три линии:

Пунктирная серая линия на графике — это так называемая Null hypothesis, отражающая состояние H=0,5 (условное обозначение, в виде линии, некоего абсолютный хаоса). Фишка в том, что если бы изменения цены котировок (красная толстая линия) были бы полностью хаотичными (H=0,5), ее экспонента лежала бы на графике точно вдоль пунктирной линии.

Как мы видим, экспонента Херста (красная толстая линия) как бы обвивает серую нуль-линию, то удаляясь от нее, то приближаясь; при этом она расположена к ней очень близко, что затрудняет визуальную работу с экспонентой. Третья линия V Stat - предназначена для определения стохастического цикла, того временного предела, о котором “помнит” биржа. Подробней о ней будет сказано ниже.

Чтобы облегчить задачу работы с экспонентой Херста, в левом верхнем углу диаграммы расположена динамическая система координат, позволяющая нам ориентироваться по экспоненте Херста (ее отличиям от нуль-линии):

Здесь изначальное статическое значение Н=0,5 представляет основное состояние экспоненты (серая пунктирная линия), соответствующее чистому броуновскому движению (т.е. обозначает абсолютный хаос).

Динамически изменяющееся (вслед за перемещением курсора по шкале) значение соотвествует горизонтальной (нижней) шкале диаграммы, отмечающей временной диапазон вероятных циклов (в днях или барах - это выбираем в настройках X Scale). При это данное значение всегда будет в днях, даже если настройки шкалы - в барах:

Динамически изменяющееся (вслед за перемещением курсора по шкале) значение соотвествует красной регрессионной линии, отмечая более персистентные зоны.

Динамически изменяющееся (вслед за перемещением курсора по шкале) значение соотвествует синей регрессионной линии, отмечая менее персистентные зоны.

Самое главное в диаграмме, это отличия толстой красной R/S-линии от серой нуль-линии и значения ее наклона к ней. В целом:

Значение близкое к 0,5: красная R/S-линия очень близка к нуль-линии, а ее наклон очень близок к значению 0,5. Это значит, что наблюдаемые циклы характеризуются хаотичностью и случайностью процесса.

Значение H больше 0,5: значение наклона R/S линии выше, чем 0,5, и одновременно красная толстая линия выше серой нуль-линии - здесь мы имеем дело с персистентностью временных рядов. Это позитивное значение - в данное время движение рынка зависит от предыдущих движений (циклы имеют привязку к эффекту памяти).

Значение H меньше 0,5: значение наклона R/S линии ниже, чем 0,5, и одновременно красная толстая линия практически “легла” на серую нуль-линии, или даже ниже ее - здесь мы имеем дело с анти-персистентностью временных рядов (т.е имеем дело с анти-трендом). Очень часто в это время случается отскок от основного тренда.

Таким образом, можно сказать, что анализ масштабируемого диапазона позволяет выявить тренд и цикл, пребывающий в скрытом виде.

Пример с R/S diagram

На графике масштабируемого диапазона экспоненте реальной цены соответствует красная линия — это ее R/S диаграмма (то есть реальные значения экспоненты Хёрста). Например, на диаграмме, что ниже мы видим, что красная линия расположена выше нуль-гипотезы в диапазоне от 5 до 50 дней по оси Х.

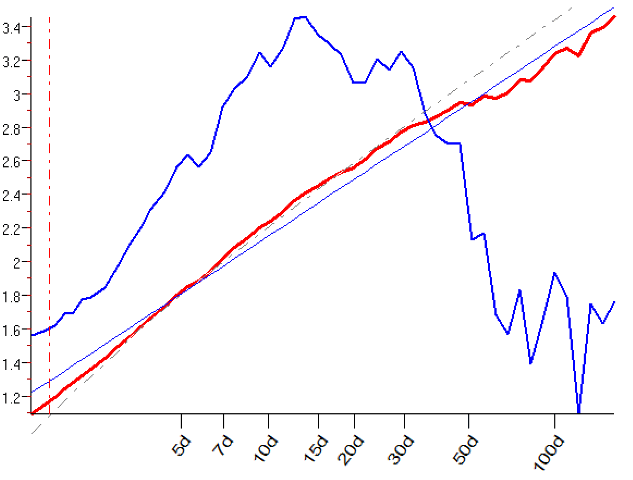
Это означает, что во временных рядах больше 7 и меньше 50 дней цена (именно ее мы анализируем: сам график цены изображен в нижней части окна) обладает «эффектом памяти», то есть придерживается в своем движении определенных устойчивых тенденций, отличных от полной хаотичности. Выше 50 дней наблюдается обратная реакция и в этом случае говорят, что проявляется антиперсистентность, когда рынок стремится не уподобляться предыдущим тенденциям, а компенсировать их в обратном направлении.

Чем выше красная линия над пунктирной, тем больше значение экспоненты Херста и тем выше персистентность (= тенденциозность) в ценовом движении.

V Stat. Стохастический цикл

Самое ценное на нашем графике — синяя линяя (т.н. V Stat), которая позволяет определить так называемый стохастический цикл. Что это такое? Если быть кратким, стохастический цикл — это длина памяти рынка, то есть продолжительность времени, на протяжении которого рынок «помнит» о своих изменениях, тенденциях и закономерностях.

Понятие стохастического цикла позволяет нам внести ясность в осмысление рыночных ситуаций, когда вроде бы предсказуемое поведение неожиданно перестает таковым быть и все ранее отмеченные закономерности ценовых изменений больше не действуют. Теперь-то мы понимаем: дело не в том, что наша торговая система перестала «работать», а в том, что рынок вошел в новый стохастический цикл.

При этом иногда бывает, что сигналы нашей системы на покупку начинают приносить прибыль, если их интерпретировать прямо противоположным образом (то есть по сигналу «покупать» нужно продавать, а по сигналу «продавать» — покупать); это и есть проявление антиперсистентности (H < 0,50) в чистом виде.

Точка по оси Х, в которой V Stat (синяя линяя) кульминирует относительно нуль-гипотезы (пунктирной линии), как раз и указывает нам на стохастический цикл, который реализуется на рынке в момент анализа.

Опции и настройки в Hurst Exponent

Поле Index

Здесь мы выбираем индекс, которым будут обработаны котировки. По сути, это тоже своего рода осциллятор, но у теории Хаоса есть своя специфика, поэтому используется свой индекс для обработки данных. По умолчанию - Ln Gain.

Поле Index Periodogram

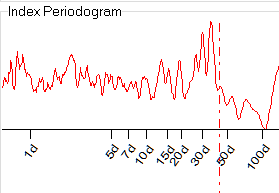
Здесь здесь выбранный индекс отображается в виде периодограммы.

Поле Algorithm

Здесь задается алгоритм, при помощи которого производится оценка фрактальной размерности временных рядов.

Собственно, сам алгоритм выбирается через выпадающее меню:

R/S - это родной алгоритм теории Херста (рекомендуемый вариант, задан по умолчанию). Показатель Херста связан с коэффициентом нормированного размаха (R/S), где R – размах временного ряда, а S – его стандартное отклонение. В свое время Херст экспериментально определил, что для многих временных рядов справедливо:

R/S = (N/2)^H, где N – длина временного ряда.

Именно коэффициент H известен как показатель Херста, представляющий собой меру персистентности – склонности процесса к трендам.

DFA - детрендовый анализ флуктуаций (DFA)представляет собой метод для определения статистической самоподобности (self-similarity) некоторого ряда данных. При анализе временных рядов это полезно для оценки таких процессов долгосрочной памяти, как расходящееся время корреляции.

Полученные показатели будут во многом аналогичны R/S-алгоритму, за исключением того, что алгоритм DFA может быть также применен к временным рядам (и возможно, сработает лучше), чьи основные статистические показатели (например, среднего значения и дисперсии) или чья динамика являются нестационарными (меняются со временем).

О математике DFA подробнее можно почитать здесь: https://en.wikipedia.org/wiki/Detrended_fluctuation_analysis

О самоподобии здесь: https://ru.wikipedia.org/wiki/Самоподобие

Поле Index View

Здесь мы видим визуальное проявление обработки котировок выбранным индексом.

Меню X Scale

Выпадающее меню X Scale позволяет настроить отображение нижней горизонтальной шкалы в днях или барах.

Вкладка Phase Space

Фазовое пространство (Phase space) представляет собой множество всех возможных состояний динамической системы в фиксированный момент времени. Каждому из них соответствует некоторая точка в фазовом пространстве. Тогда состояние сколь угодно сложной системы можно представить одной единственной точкой в фазовом пространстве, а ее эволюцию – траекторией перемещения этой точки.

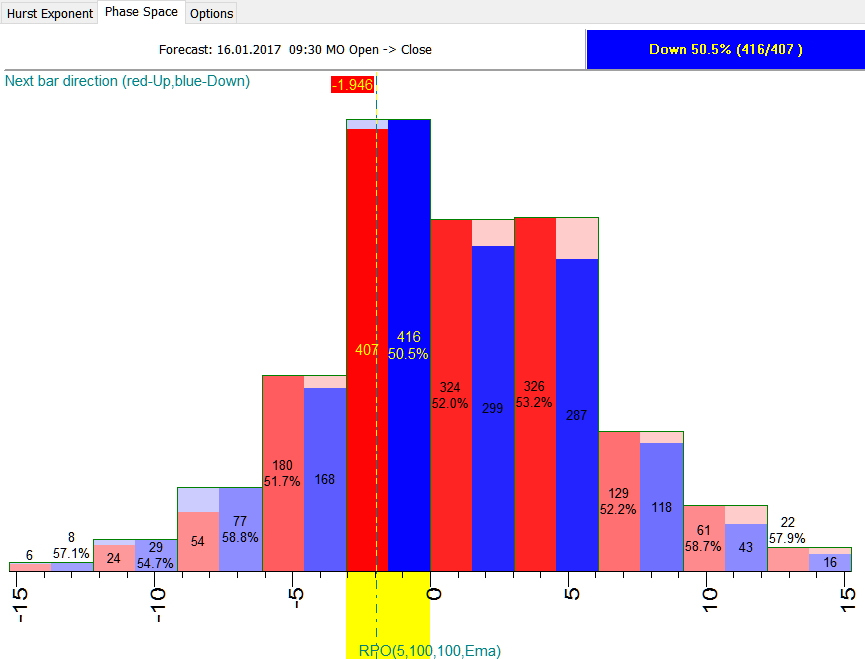
Теоретически, это можно попытаться использовать в прогностических целях:

Однако, на данным момент это носит больше эксперементальный характер; в модуле Chaos Teory мы рекомендуем сосредоточиться на работе с Hurst Exponent.

Практическое применение Теории Хаоса в трейдинге

Теория Хаоса, в целом, довольно сложна. И первое что нужно уяснить, она не предназначена для получения прогнозов впрямую: если мы попытаемся использовать экспоненту Херста непосредственно для выявления тренда, мы потерпим фиаско. Однако, этот модуль может дать нам бесценную информацию, используя которую мы можем улучшить прогностическую работу в других модулях Timing Solution:

- Херст может помочь нам в выявлении стохастического цикла. Иначе говоря, при помощи теории Хаоса мы можем прояснить такую утилитарную вещь, котировки какой длинны оптимальны для выявления циклов в исследуемом торговом инструменте

- наконец, при работе с циклами мы получаем инструмент, позволяющий оценить валидность циклов той или иной периодичности.

Как получить эту информацию? На практике повседневное ее применение можно свести к нескольким простым правилам:

- посмотрите, где именно красная толстая линия находится выше серой нуль-линии. Отметили? В этих местах (например, с 10 до 30 баров) будут возникать самые сильные циклы в поддержку тренда. Это наблюдение можно использовать в работе с другими модулями, например с Q-Spectrum.

- там где красная линия ниже серого пунктира - соотвественно, все наоборот. Здесь вероятны отскоки, обратные, перевернутые циклы; к циклам, которые будут появляться в этой зоне, нужно относиться с осторожностью. В целом, там где циклы данной периодичности будут появляться, на рынке весьма вероятна сильная волатильность.

- наконец, самое главное, отметьте места максимумов синей толстой линии V Stat. Это самая ценная информация. Максимум может быть один, а может и два, как на этом примере:

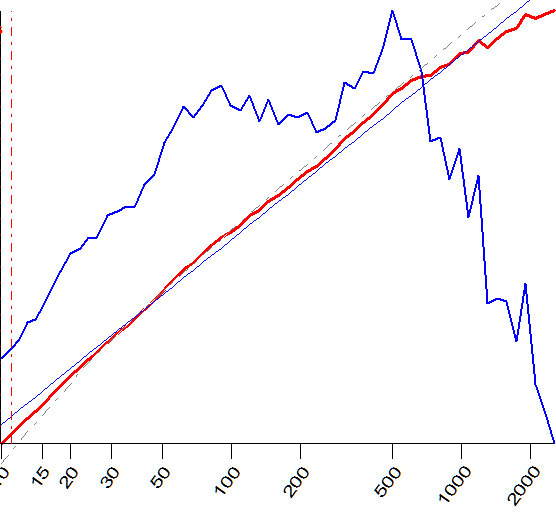
Отметьте самый дальний максимум. На рисунке (используются часовые бары) это будет район 500-600 баров. Здесь заканчивается память биржи. Циклы, находящиеся в этой зоне (до 500-600 баров) - валидны, вне ее - лучше, вероятно, не использовать (применяем данную информацию при работе с этими котировками в других модулях).

Использование теории Хаоса в нейросети

По умолчанию в Timing Solution в качестве интервала обучения нейросети используются все доступные данные. Это, однако, создает трудности, поскольку, как мы увидели, из примера выше, рынок в часовом таймфрейме «не помнит себя» старше 500 баров Следовательно, всякий раз, как нейросеть в процессе обучения будет забирать со своих входных узлов изменения котировок старше 500 баров, вместо полезной информации в сеть будет подаваться в лучшем случае шум, в худшем — данные, искажающие реальную картину.

Как применить полученное знание в нейросети? Зайдите в модуль Neural Net, измените опцию ALL (то есть — использование всех доступных данных для обучения сети) на тип Use Last %x Price Bars before LBC (задать число последних баров) и указываем для Use Last Price Bars значение 500 баров:

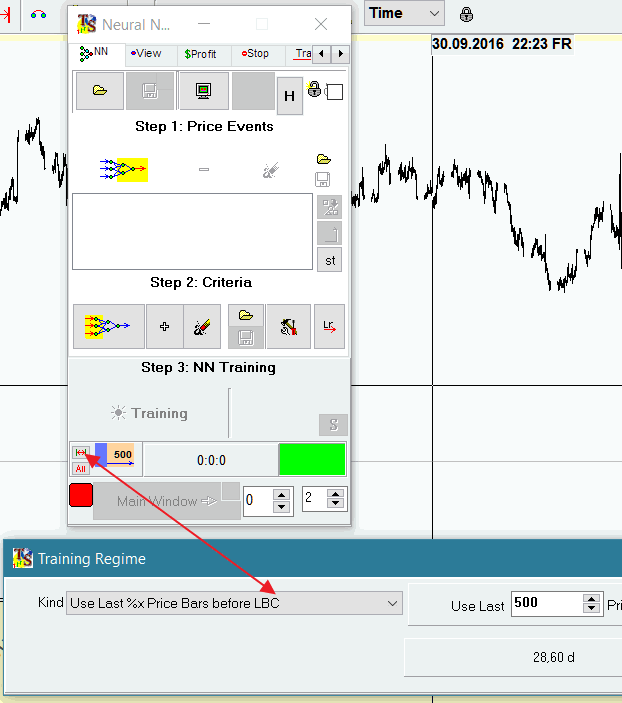
И далее, выбрав то, с чем вы будете работать в нейросети (те факторы, которые вы подаете на вход), тренируйте нейросеть с использованием данных параметров.

По такому же принципу рекомендуется работать и с другими модулями.